Le magnétisme est l'une des théories physiques souvent citées par ceux qui nous mentent


Ouvrez un livre de physique, vous y trouverez des tas d'équations, souvent complexes. Ce n'est pas pour impressionner le néophyte, c'est tout simplement que le seul but de chaque théorie physique est de calculer un phénomène, avec un résultat assez précis pour vérifier si la prédiction ainsi calculée est validée par l'expérience. Si la théorie est validée, elle peut ensuite être utilisée par des ingénieurs pour calculer les machines qu'ils vont inventer. Nous allons immédiatement voir un exemple concret.
En attendant, on peut déjà retenir que si quelqu'un prétend
utiliser des théories physiques mais qu'il n'a besoin de faire
aucun calcul, c'est qu'il ne fait en réalité pas de physique. Tout
comme on ne peut pas faire de littérature sans utiliser des mots,
on ne peut pas faire de physique sans utiliser des calculs: on
peut parfois expliquer certaines théories physiques sans faire de
calculs (ou pas beaucoup), en disait “on a calculé que...”, mais on ne peut pas les
utiliser sans faire de calculs.
Ils ne cessent de parler d'énergies, de sentir l'énergie, de la
transférer, de la débloquer. Ça ne veut pas dire grand chose, mais
en vrai c'est quoi l'énergie?
Intuitivement, l'énergie est ce qui permet à un moteur de tourner
et de propulser un véhicule ou de soulever une charge, et ce qui
permet de chauffer une maison ou une casserole. Mais cette notion
n'est devenue utile que lorsque les physiciens ont su comment
calculer l'énergie, et qu'ils ont montré la loi de la conservation
de l'énergie: l'énergie change de forme, mais la quantité totale
d'énergie reste la même.
Voici un exemple simple de calcul d'énergie et de prédiction
obtenue grâce à ce calcul.
On lance une balle en l'air, cette balle contient de l'énergie:
elle nous fera mal en nous frappant. On sait calculer l'énergie
correspondant au mouvement, qu'on appelle “énergie cinétique”,
avec cette formule:
$$E_c={1\over 2}m.v^2 $$
avec:
Donc si on lance une balle pesant
100 g à une vitesse de
10 km/h, on a \(m=0.1\), \(v=10/3.6\), et
on obtient \(E_c=0.385\): l'énergie cinétique de cette balle est
de 0.385 Joules.
Maintenant, prenons la balle et plaçons-la en hauteur. À nouveau,
elle contient de l'énergie: si on la laisse tomber, elle pourra
nous faire mal. Cette énergie s'appelle “énergie potentielle” et
est calculée avec cette autre formule:
$$ E_p = m.g.h $$
avec:
Donc si on soulève la balle pesant 100 grammes d'une hauteur de 2 mètres, on lui donne une énergie potentielle de 1.96 Joules.
Pour l'instant, ces calculs ne servent à rien, mais il est facile de les utiliser pour faire des prédictions.
Supposons que nous lançons la balle vers le haut avec une
certaine vitesse, \(v\),
et que l'on veut savoir quelle hauteur \(h\) elle va atteindre.
Au moment où la balle cesse de monter et va commencer à retomber,
il y a un instant infiniment court où elle ne bouge plus, donc
elle n'a plus d'énergie cinétique mais uniquement de l'énergie
potentielle. La conservation de l'énergie nous dit que l'énergie
cinétique du départ s'est transformée en énergie potentielle, ce
qu'on écrit ainsi:
$$ m.g.h = {1 \over 2} m.v^2 $$
Même si on ne connaît pas la masse \(m\), on sait que si les deux termes de l'égalité
sont identiques, alors ils restent identiques si on les divise
tous les deux par la même valeur \(m\), puis par la même valeur
\(g\), et ainsi l'égalité
précédente devient celle-ci:
$$ h = {v^2 \over 2g} $$
Ces calculs nous permettent donc de prédire à quelle hauteur va monter la balle.
Si on lance la balle à 10 km/h,
verticalement, nous faisons le calcul avec \(v=10/3.6\) et
\(g=9.81\), et nous obtenons \(h=0.39\), c'est-à-dire que nous
prédisons que la balle montera à une hauteur de 39 cm. Si l'expérience donne une valeur très
différente, c'est soit que la théorie est fausse et doit être
abandonnée, soit qu'il y a un problème expérimental qui doit être
élucidé.
De très nombreuses expériences ont été faites, depuis l'invention
de cette théorie par Newton à la fin du XVIIe siècle,
et ont montré sa grande exactitude (sauf pour des objets de la
taille d'un atome, ou des vitesses proches de la vitesse de la
lumière), ce qui fait qu'elle est aujourd'hui utilisée par tous
les ingénieurs qui ont besoin de lancer un objet, qu'il s'agisse
d'une fusée ou d'une pièce dans un métier à tisser.
Depuis Newton, de nombreuses autres formes d'énergie ont été
découvertes et calculées, par exemple l'échauffement d'un
matériau, la compression d'un ressort ou d'un gaz, les différents
phénomènes électromagnétiques (courants électriques, aimants,
ondes radio), l'accrochage entre les atomes d'une molécule,
l'énergie produite par les réactions nucléaires, etc... Les
calculs qui sont faits et les prédictions qui en sont tirées sont
innombrables.
Contrairement aux physiciens avec leurs calculs, les gourous des
pseudo-sciences n'ont besoin d'aucun calcul pour dire “là je sens beaucoup d'énergie”,
ou “je suis en train de
transférer vos énergies négatives”. Vous ne comprenez pas
ce qu'ils veulent dire concrètement avec ces phrases? C'est normal
car elles ne veulent rien dire du tout!
Généralement, comme les gourous ne font aucun calcul, ils
n'obtiennent aucun résultat: ils sentent “beaucoup d'énergie”,
mais ne vous dirons pas s'il s'agit d'un millionième de Joule ou
d'un milliard de Joules. Certains indiquent un résultat numérique,
par exemple “votre énergie est
à 67”, mais sans pouvoir dire comment ils peuvent dire
que cette énergie, à supposer qu'ils la “sentent” réellement, est de 67. Car bien sûr
que nous pouvons sentir certaines énergies: une personne entraînée
pourra dire avec une certaine précision quelle est la température
d'une rivière, juste en y trempant la main, mais pour cela il aura
fallu qu'elle s'entraîne à comparer sa sensation avec la mesure
donnée par un thermomètre, qui aura lui-même été étalonné pour
indiquer 0°C dans l'eau glacée et 100°C dans l'eau bouillante. Les
gourous, eux, n'ont eu besoin d'aucun appareil pour faire leur “mesure”: c'est donc de la
charlatanerie.
Plus encore que de l'énergie, les gourous affirment faire “du
magnétisme”, posséder un “fluide magnétique”, etc... Si cela n'a
pas grand sens, il est intéressant de se demander ce qu'est
réellement le magnétisme.
On connaît le magnétisme (les aimants) et l'électricité statique
depuis toujours, mais c'est au XIXe siècle que les
physiciens ont compris que c'était deux aspects de
l'électromagnétisme, et qu'ils réussi à écrire les quatre
équations qui permettent de les calculer très précisément. Ce sont
les “équations de Maxwell”, que voici:
$$ \mathrm{div}\ \overrightarrow E = {\rho \over \varepsilon_0} $$
$$ \overrightarrow{\mathrm{rot}}\ \overrightarrow E = -\frac{\partial \overrightarrow B}{\partial t} $$
$$ \mathrm{div}\ \overrightarrow B = 0 $$
$$ \overrightarrow{\mathrm{rot}}\ \overrightarrow B = \mu_0 \left[ \overrightarrow j + \varepsilon_0 \frac{\partial \overrightarrow E}{\partial t}\right] $$
Les vecteurs \(\overrightarrow E\) et \(\overrightarrow B\) sont
le champ électrique et le champ magnétique, et ces équations
indiquent comment les charges électriques provoquent un champ
électrique, comment les courants électriques provoquent un champ
magnétique, et comment les variations du champ magnétique
provoquent un champ électrique et réciproquement, ceci expliquant
la propagation des ondes radio et de la lumière. On peut faire une
infinité de calculs (souvent un peu compliqués) avec ces
équations.
Cette théorie est utilisée par les ingénieurs avec un immense
succès, par exemple pour la fabrication de moteurs électriques,
d'émetteurs et de récepteurs sans fil et de leurs antennes.
Une branche de l'électromagnétisme concerne les matériaux
magnétiques, c'est-à-dire ceux dans lesquels un champ magnétique
significatif est créé par la rotation des électrons autour des
atomes, en particulier les matériaux “ferromagnétiques” (comme le
fer), qui peuvent s'aimanter très fortement. Certains s'aimantent
fortement quand on les place dans un faible champ magnétique,
c'est le cas du fer pur (fer doux), qu'on utilise pour fabriquer
des moteurs électriques et des transformateurs. D'autres restent
aimantés même hors de tout champ magnétique: ce sont les
“aimants”. Mais la plupart des matériaux, qui ne sont ni
ferromagnétiques ni des aimants, sont à peu près insensibles à
tout champ électrique.
Sans utiliser le moindre courant électrique, ni aimant, ni
matériau ferromagnétique, les gourous vous affirment “je fais du magnétisme pour vous
soigner”. Ceci est plutôt vague, mais c'est surtout
complètement faux et hors de propos: puisque le corps du gourou ne
peut produire aucun champ magnétique notable, et que le corps de
son client est à peu près insensible aux champs magnétiques, il
est clair qu'un gourou apposant ses mains sur son patient ne peut
en réalité rien faire qui soit “magnétique”. Ce qu'il peut faire
est apporter la chaleur de ses mains, la pression de ses mains, du
réconfort grâce au contact physique, mais assurément aucun “fluide
magnétique” (qui n'existe d'ailleurs pas en physique).
Les gourous voient partout des bonnes ou des mauvaises ondes, et
des vibrations. Oui mais de quoi parle-t-on?
En physique, une onde est une vibration qui se propage, comme les
vagues à la surface d'un lac. La propagation résulte de la
transformation continuelle entre deux formes d'énergie: par
exemple dans une vague, l'eau est alternativement placée en haut
de la vague (énergie potentielle), et propulsée vers le haut ou le
bas de la vague (énergie cinétique). De nombreuses ondes sont bien
connues:
Parmi les caractéristiques d'une onde, on mesure habituellement sa fréquence \(f\) (le nombre de vibrations par seconde, en Hz), sa vitesse de propagation \(c\) (pour “célérité”: 320 m/s pour le son dans l'air, 300 000 km/s pour la lumière), et sa longueur d'onde \(\lambda\) (on utilise la lettre grecque “lambda”, mais si on la notait \(L\) ce serait pareil). La longueur d'onde se calcule ainsi: \(\lambda=c/f\).
Ces caractéristiques permettent de faire de très nombreux calculs dans de nombreux domaines, par exemple sur la réfraction optique. Ce que les opticiens appellent “indice optique” d'un verre est la facteur de réduction de la vitesse de la lumière dans ce verre, par rapport à la vitesse de la lumière dans le vide. La longueur d'onde étant modifiée lorsque la lumière pénètre dans le verre ou en ressort, la direction du faisceau est déviée comme indiqué ci-dessous: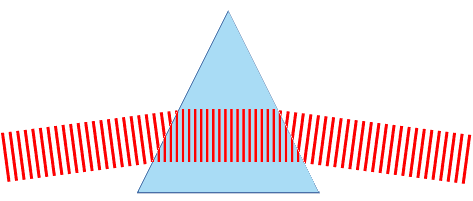
La réfraction se calcule avec les formules de Descartes, de façon
très simple:
$$ n_1.\sin{\theta_1} = n_2.\sin{\theta_2} $$
avec \(n_1\) et \(n_2\) les indices optiques d'un côté et de
l'autre de l'interface, \(\theta_1\) et \(\theta_2\) les angles
d'incidence du faisceau de chaque côté par rapport à
l'interface; “\(\sin\)” est la fonction mathématique “sinus”.
On voit qu'il suffit de savoir que la lumière est une onde et que
sa vitesse dépend du matériau pour prédire de quelle manière la
lumière va changer de direction en entrant dans un matériau
transparent.
L'expérience montre que la lumière se propage effectivement ainsi
dans la grande majorité des matériaux, la théorie est donc
utilisée pour fabriquer des lunettes, et des lentilles pour toutes
sortes d'appareils optiques.
Les ingénieurs qui fabriquent des appareils médicaux utilisent et
calculent différents types d'ondes: la lumière pour les
microscopes, les rayons X et gamma dans les scanners à rayons X et
les PET-scan, les ondes acoustiques dans les échographes, les
ondes électromagnétiques dans les appareils d'IRM.
Les médecins n'ont pas le temps de faire des calculs de physique
quand ils soignent leurs patients, même avec ces appareils qui
utilisent des ondes. Il leur arrive donc de dire “ondes” pour
parler des ondulations d'une courbe (même si ce n'est pas une
“onde” pour les physiciens).
De même, quand les cardiologues parlent “d'onde Q” ou “d'onde T”,
ce sont des bosses ou des creux sur les courbes d'un
électrocardiogramme, qui retranscrit les variations des courants
produits par l'activité du cœur. La position de ces bosses aide à
savoir si le cœur fonctionne normalement.
Pour les gourous, les ondes ne sont ni acoustiques ni
électromagnétiques, et elles ne correspondent pas non plus aux
ondulations d'un enregistrement. Non, elles sont bien plus vagues:
il y aurait de “bonnes ondes”,
des “ondes hostiles”
(celles de l'observateur méfiant prêt à démasquer le truc d'un
charlatan), des “bonnes
vibrations” (ce qui n'est réel que s'il joue de la
musique: le son est bien une vibration et une onde, et il arrive
qu'il soit agréable). Ils affirment que “tout vibre continuellement”: certes tout bouge,
en particulier avec l'agitation thermique, mais cela se mesure
sans aucun don particulier, juste avec un thermomètre.
Donc pour les gourous, les “ondes” et les “vibrations” sont la
fausse promesse qu'ils ont un don magique. Ceci n'a bien sûr rien
à voir avec un phénomène ondulatoire, ni avec quoi que ce soit de
mesurable: ce n'est que le langage creux d'un charlatan.
Il est très commode pour les gourous de parler de “quantique”, car la mécanique quantique est une branche récente de la physique (découverte au cours du XXe siècle), et que très peu de personnes comprennent car les calculs sont souvent difficiles, les résultats plutôt déconcertants pour les débutants, et le domaine d'application limité à des objets de dimension microscopique.
Du coup, c'est paradoxalement pratique: si on vous parle de
“quantique”, hors des domaines réels d'applications de la
mécanique quantique (la microélectronique, les lasers, etc), vous
pouvez parier qu'il s'agit d'un charlatan.
La mécanique quantique est une méthode de calcul, dont les bases
théoriques ne sont d'ailleurs pas totalement satisfaisantes, qui
permet de prédire très précisément comment se comportent les
objets microscopiques (à l'échelle de l'atome).
Le principe de base est que les particules se propagent
exactement comme des ondes, et donc que le mouvement d'un électron
n'est pas très différent de celui d'un faisceau lumineux,
simplement l'onde n'est pas régie par les équations de Maxwell
mais par une autre: l'équation de Schrödinger. Toutefois,
lorsqu'on cherche à mesurer ces particules, elles perdent
subitement leur aspect ondulatoire et redeviennent des particules
détectées à un endroit précis.
Une expérience historique est celle des fentes d'Young: en envoie
des électrons sur une 1ère plaque percée d'une fente,
derrière laquelle on met une 2e plaque percée de 2
fentes, et encore derrière on met un écran fluorescent qui détecte
les électrons. On constate que les électrons qui traversent la 1ère
fente repartent dans plusieurs directions, et de même pour les 2
fentes de la 2e plaque, ce qui ressemble au phénomène
de diffraction pour les ondes. Mais surtout, il se produit une
figure d'interférence (une alternance de zones recevant plus ou
moins d'électrons) sur l'écran fluorescent, avec une forme qui
dépend de l'écartement entre les 2 fentes.
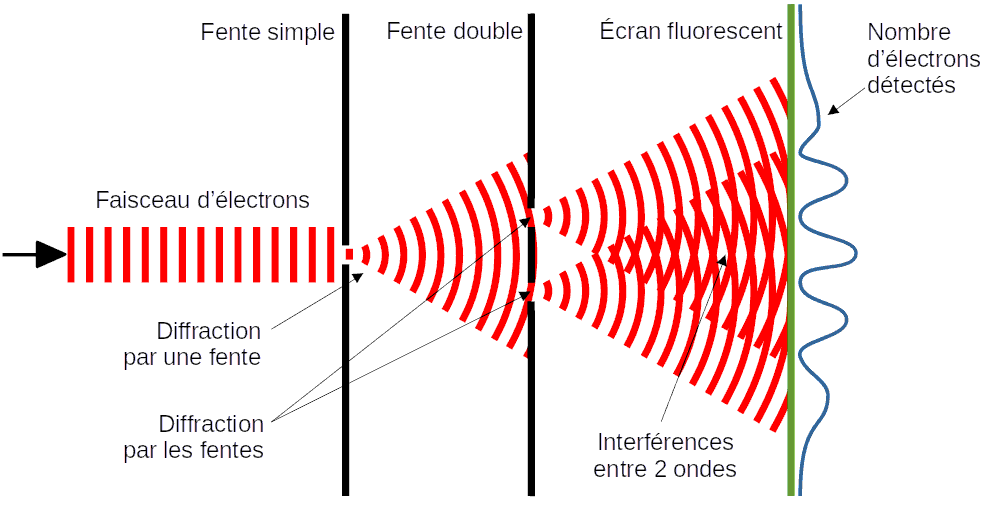
La diffraction dans les fentes, mais surtout la figure d'interférence, montre qu'il y bien 2 ondes émises par les 2 fentes de la 2e plaque. La mécanique quantique prédit cela et permet de le calculer, et cela n'a rien d'intuitif, puisque cela signifie que les électrons se propagent comme une onde, et que chaque électron est passé à la fois par les 2 fentes de la 2e plaque (sinon la figure d'interférence ne pourrait pas dépendre de l'écartement entre les fentes).
Des expériences ont prouvé qu'il n'y a pas à la fois une onde et
une particule, mais que c'est bien une particule matérielle qui se
propage comme si elle était une onde, jusqu'au moment où on
détecte sa position. C'est un peu troublant, mais les équations
fonctionnent admirablement: on prédit exactement l'endroit où
arrivent les électrons, et beaucoup d'autres phénomènes bien plus
complexes.
Tout aussi troublant que de voir les particules de matière se
propager comme des ondes, la mécanique quantique montre que les
ondes peuvent se comporter comme des particules. Ceci est très
bien connu dans les ondes électromagnétiques, qui se propagent
bien selon les lois de l'électromagnétisme (les équations de
Maxwell), mais qu'on ne peut pourtant émettre ou détecter que sous
la forme de petits grains de lumière qu'on appelle “photons”.
Aussi troublant que ce soit, nous y sommes aujourd'hui habitués
car nous disposons de capteurs capables de détecter un unique
photon, par exemple dans les LIDAR (genre de radar qui fonctionne
avec une lumière infrarouge). Les radiologues aussi y sont
habitués, car les rayons X (qui sont également des ondes
électromagnétiques) arrivent aussi sous forme de photons, qui
donnent un aspect bruité aux radiographies.
Le terme “mécanique quantique” vient de ce qu'on décrit les
mouvements de la matière (“mécanique”) et que certaines grandeurs
deviennent quantifiées (par exemple pour la lumière, on détecte
0 photon, 1 photon, 2 photons,
etc..., mais on ne peut pas détecter 0.5 photon, même si on baisse
la puissance de la lampe).
Dans la mécanique “classique” (c'est-à-dire non quantique), il y
a déjà une quantification pour la fréquence des ondes qui se
propagent dans un espace limité, c'est-à-dire que seules certaines
fréquences sont possibles. Par exemple si une corde de piano est
accordée sur la note “do”, elle résonne également dans les
fréquences multiples de cette fréquence (on appelle “fondamentale”
la note principale, et “harmoniques” les fréquences multiples). Si
la fondamentale est la note do3, les harmoniques sont
les notes do4, sol4, do5, mi5,...
Par contre, dans la mécanique classique, la puissance de la note
peut avoir n'importe quelle valeur, jusqu'à l'infiniment faible.

Il en est de même pour les vibrations dans un tuyau (un clairon
ne peut jouer que certaines notes), ou pour la lumière dans une
couche fine transparente (ce qui produit les irisations des bulles
de savon).
La mécanique quantique indique que la matière se propage comme
une onde, dont la fréquence est quantifiée comme toute onde
lorsqu'elle est dans un espace limité. La conséquence est que les
propriétés de la matière (par exemple l'énergie) sont alors
quantifiées.
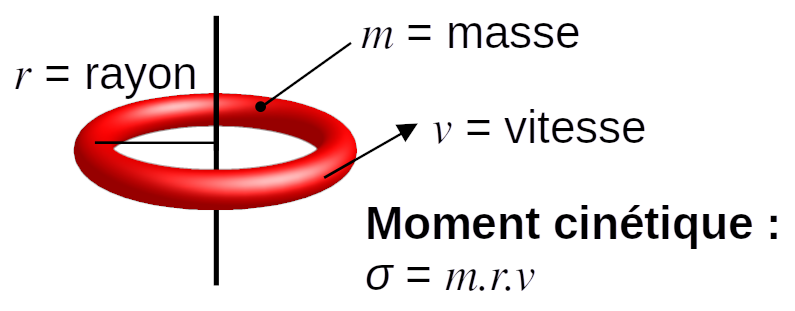
Par exemple, pour mesurer la quantité de rotation, les physiciens
calculent le “moment cinétique”, souvent indiqué par la lettre
grecque \(\sigma\) (sigma). La formule est particulièrement simple
pour un anneau en rotation, puisqu'on multiplie la masse par le
rayon et la vitesse du mouvement. Ce moment cinétique peut prendre
n'importe quelle valeur.
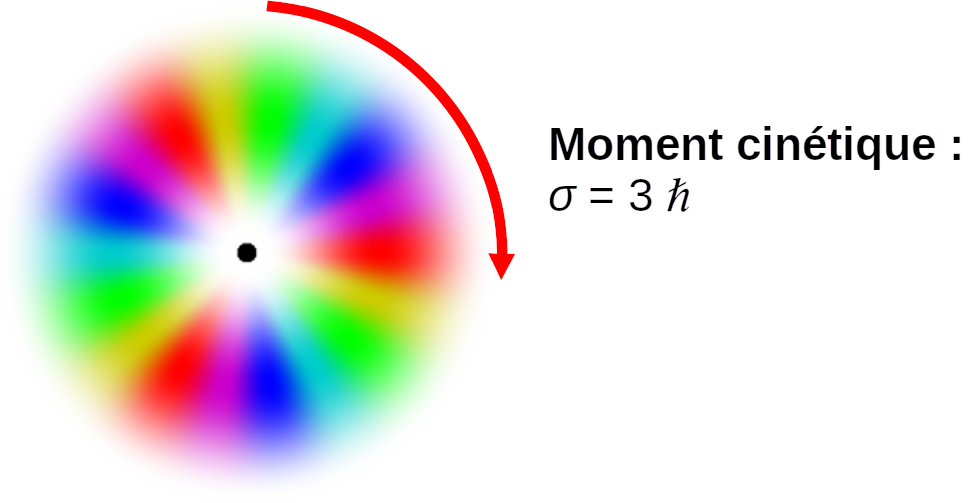
Mais dans la mécanique quantique, lorsqu'une particule tourne
autour de quelque chose, son mouvement est décrit par une onde
autour du centre de la rotation, et le nombre de périodes de
l'onde ne peut être qu'un nombre entier. Pour cela, le moment
cinétique est forcément un multiple d'une certaine valeur, la
“constante de Planck” (notée \(\hbar\) et prononcée “H barre”, sa
valeur est absolument minuscule: \(\hbar=1.05 \times 10^{-34}\) m2.kg/s).
De même, l'énergie des particules bloquées dans un espace limité
ne peut prendre que certaines valeurs, qu'on appelle “niveaux
d'énergie”.
On peut citer plusieurs cas de quantification de l'énergie:
Les électrons d'un atome, retenus l'attraction du noyau: ils ne peuvent avoir que certains niveaux d'énergie. Pour l'atome d'hydrogène (le plus simple), l'énergie ne peut avoir que les valeurs \(-E_0/n^2\), où \(E_0\) est l'énergie de liaison (13.6 électron.volts) et \(n\) est un entier supérieur à 0. Ceci explique que chaque atome ait des raies d'absorption de la lumière bien précises.
Pour les gourous, qui ne connaissent pas les calculs de la
mécanique quantique, et qui ne veulent de toute façon pas les
expliquer à leurs adeptes, le mot “quantique” est juste une
formule magique qui permet de dire “Je maîtrise beaucoup de choses que vous ne comprenez
même pas”. Il n'y a rien derrière, ce n'est qu'une pure
charlatanerie.
Les gourous adorent parler de mécanique quantique car:
Ils savent que cette théorie n'est connue que de très peu de personnes.
La plupart des gens n'en ont aucune compréhension intuitive. Les gourous ne choisissent pas la thermodynamique, car bien que peu de personnes en maîtrisent les calculs, presque tout le monde comprend qu'on peut faire chauffer une chaudière, produire de la vapeur sous pression, faire tourner une turbine, etc... C'est parce que la mécanique quantique ne s'applique qu'à des objets microscopiques, et donc très peu de gens en perçoivent les effets, en-dehors de quelques scientifiques et ingénieurs.
La vulgarisation de la mécanique quantique est très médiocre, car cette théorie est très difficile à expliquer sans présenter les calculs, or ces calculs sont trop complexes pour être expliqués dans des ouvrages de vulgarisation.
La plupart des gens n'ont entendu parler de la mécanique quantique que comme une théorie bizarre où tout se comporte de façon incroyable, d'une manière qui choque l'intuition. Ceci est mis à profit par les gourous pour dire “puisque la mécanique quantique prouve qu'il se passe des choses incroyables, vous devez me croire quand je vous dis des choses qui vous semblent invraisemblables”. En quelque sorte, la mécanique quantique joue le même rôle que l'homéopathie (voir l'article) pour les pseudo-médecines: “L'homéopathie fonctionne et la science ne comprend pas comment c'est possible, c'est pareil pour ma thérapie très coûteuse, croyez-moi même si ça semble invraisemblable” (la différence est que la mécanique quantique fonctionne réellement, même si ce n'est pas ce que prétendent les gourous, tandis que l'homéopathie ne fonctionne pas).
Les théories physiques sont des méthodes de calcul qui permettent de prédire certains phénomènes, et dont on a validé la performance en vérifiant que les expériences donnent le résultat prédit par les calculs théoriques.
On peut vulgariser certaines théories, pour faire comprendre leur
utilité aux néophytes, avec pas ou peu de calculs, mais si on veut
les utiliser, alors il faut faire les calculs, parfois simples et
parfois compliqués.
Lorsque quelqu'un, en particulier une personne qui prétend
soigner, utilise des mots de la physique moderne hors de son
domaine d'application, et bien sûr sans jamais faire aucun calcul,
il est plus que probable que c'est un charlatan. Si de plus il
utilise le mot “quantique”, cette conclusion est même presque
certaine, car c'est un terme “moderne” et très mal compris du
grand public, et donc très utilisé par les gourous des
pseudo-sciences.